カメラのレンズ基礎知識入門という事で、レンズに関する基礎を記載していきたいと思います。今回は、分かってそうで分からないレンズの収差(球面収差,像面湾曲,非点収差,歪曲収差,コマ収差,軸上色収差,倍率色収差)を題材に、またそれに関係のある、スネルの法則に関して説明していきます。カメラ好き、レンズ好き、エンジニアの方向けに分かりやすく記載していきたいと思います。
スネルの法則と収差
スネルの法則とは、各パラメータを下図の様に定義すると、
n*sinΘ = n’*sinΘ’
であり、このようにレンズ面の屈折は計算する事が出来ます。
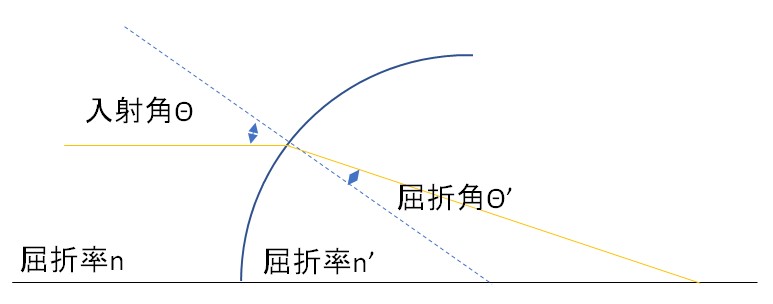
ここで、最も難しい点は、例えば平面に対する入射の場合、入射光線と境界面の交点位置が動いても、入射角や屈折角は同じですが、レンズのような球面の場合、交点の位置によって、入射角が変化し、それに伴い屈折角も変化するところです。
また、光軸から距離が離れれば離れるほど入射角が大きくなる為、大きく屈折されます。この、入射角が大きくなるとより多く屈折される。という現象により、理想の光線からのズレが生じてきます。このズレの事を収差と呼びます。
収差の発生原理
上のトピックで説明したように、入射角が大きくなると、光線は強く屈折されるという現象により収差が発生します。
この理想と現実の差が収差と呼ばれており、理想的な光線の考え方を、近軸理論と呼びます。また、この理想的な光線の考え方に基づいた、光線追跡の事を近軸光線追跡と呼ばれます。
逆に、実際の光の通り方の事を、実光線追跡と呼びます。
■近軸光線追跡
入射する光線幅が狭い時、各レンズ面に入射する入射角Θが小さい為、sinΘ≒Θ、sinΘ’≒Θ’ が成立する。この近似が成立する領域を近軸領域と呼び、それに基づく光線追跡が近軸光線追跡と呼ばれ、そこでは収差は発生しない。
■実光線追跡
上記の近軸光線追跡に対し、光線が広がりをもつと、sinΘ = Θ、sinΘ’ = Θ’ が成立しなくなる為、収差が発生する。入射角が大きくなればなるほど、近軸光線追跡から外れ、収差量が大きくなる。
つまり、入射角が狭いと、スネルの法則の通りに計算できるが、入射角が大きくなってくると、理想的な計算が出来なくなり、その結果、焦点がズレるような現象が起き、収差が発生する。という事です。
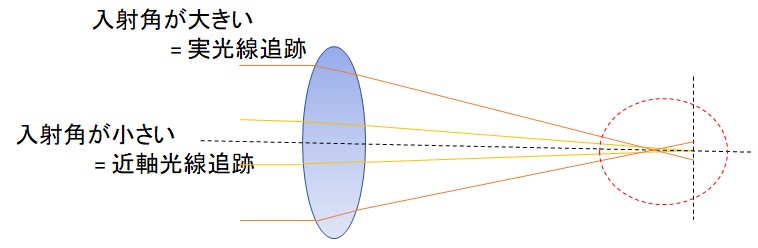
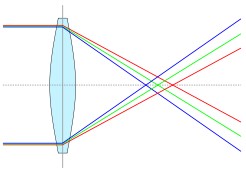
図で書くと下のようになり、黄色の光線は入射角が小さく、理想的な光線となり、ピントもあっている近軸光線追跡となり、オレンジの光線は、入射角が大きく、理想的な光線にならず、ピントもズレてしまう、実光線追跡となります。
収差の種類
それぞれの収差について、ごく簡単に説明していこうと思います。
球面収差
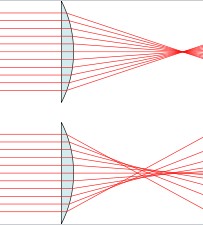
球面を含む光学系において、点光源からの光線が焦点に収束せずばらつく収差の事。下の図の上が理想的な結像イメージ、下の図が球面収差が発生し、結像位置がずれてしまったイメージです。
像面湾曲
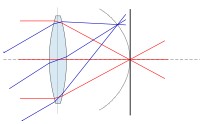
光学系に平行な焦点面が平面に対応しないという収差。下の図だと、右側に縦にひかれた直線が理想的な像面となりますが、周辺部がレンズ側に寄るような形でそれぞれ湾曲してしまう現象。
非点収差
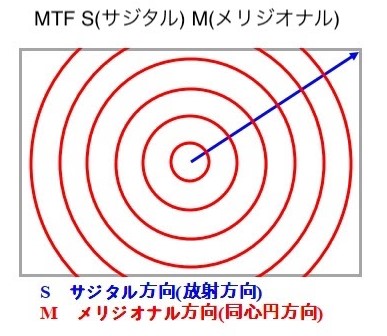
光軸外の1点を光源とする光が、レンズに対して同心円方向と直径方向(放射方向)で焦点距離がずれる収差。
同心円方向、直径方向(放射方向)とは下の図のイメージです。
歪曲収差
入射角度に対する、理想像高と主光線の実像高のズレによって生じる収差です。
典型的なあらわれかたとしては、撮像面(イメージセンサ等)に並行な被写体面のテストパターン等の矩形が矩形として撮影されない、あるいは同じ光学系を逆方向に使い投影した時にテストパターン等の矩形が矩形として投影されない、といったような収差です。
中心部が膨らむようなゆがみにより矩形が樽型になるものと、逆に中心部が収縮するようなゆがみにより矩形が糸巻き型になるもの、以上の2つに基本的には分類できますが、中心部と周辺部でこの両者が組み合わさった陣笠型などと呼ばれる歪みかたになるものもある。
イメージの1つとして下の図のような歪み方があります。

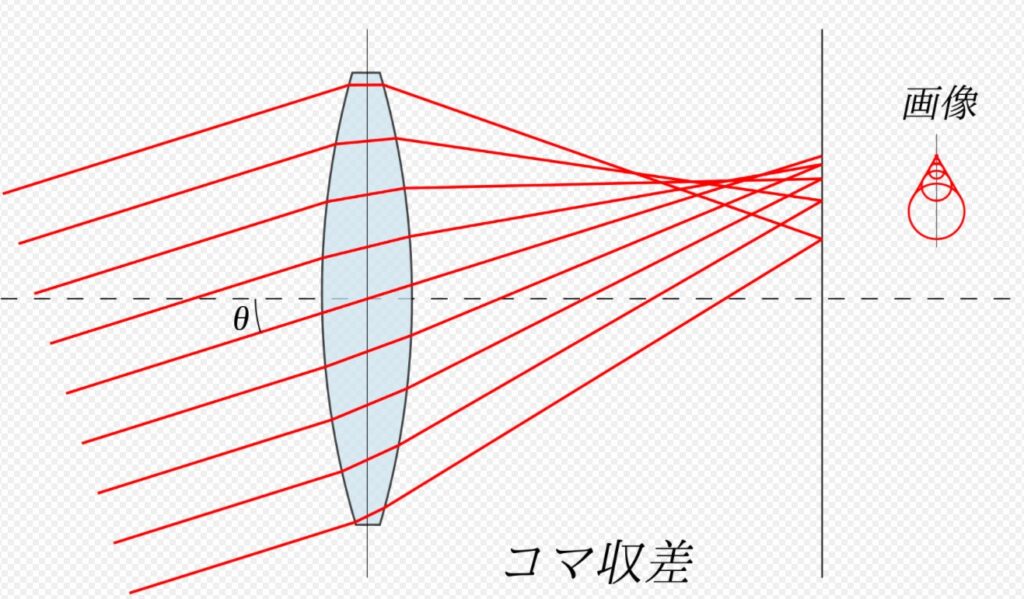
コマ収差
光軸外の1点を光源とする光が、像面において1点に集束しない収差。下のようなイメージです。
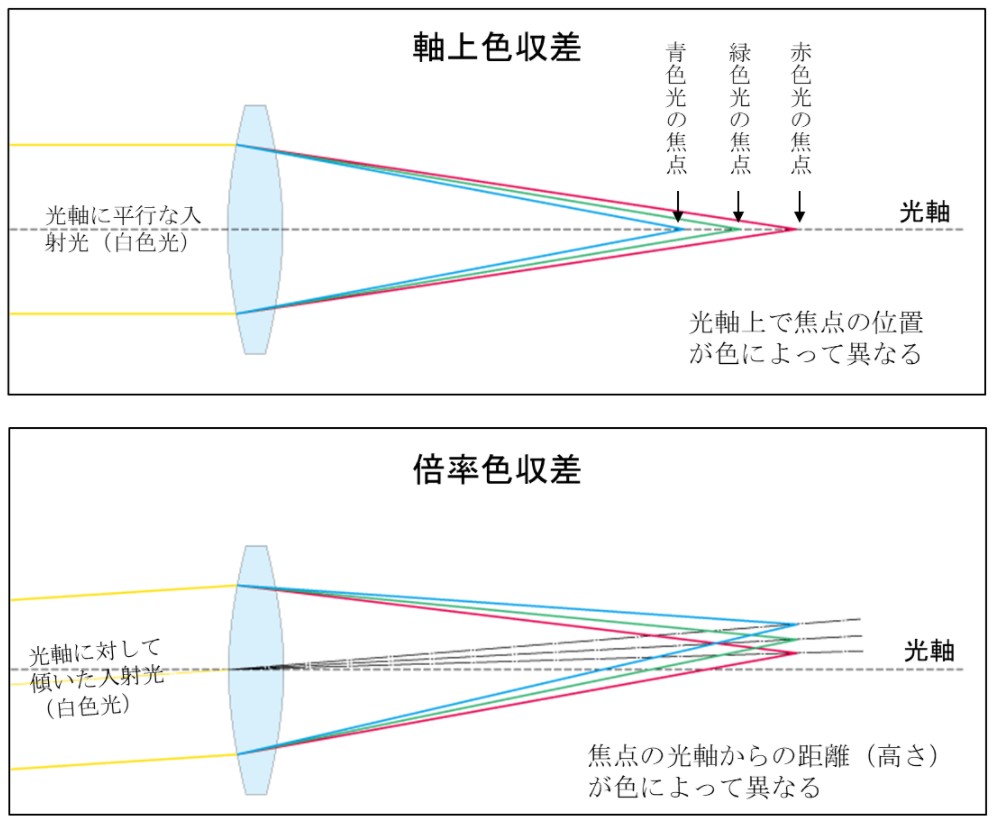
軸上色収差
色による屈折率の違いにより、結像位置が色によって前後にずれる収差。例えば白色点光源を撮影した場合、青でピントを合わせると青白い輝点のまわりに赤いボケが出来、赤でピントを合わせると赤っぽい輝点のまわりに青紫のボケができる。
倍率色収差
色による屈折率の違いは、斜めに入射した光の場合には像の倍率の違いとなってあらわれる。その結果、色により像の大きさが異なってしまい、被写体のフチに赤や青紫の色ズレが見える。白色点光源では、画面の周辺部において虹色に分解されて放射方向に伸びた像となる。
倍率色収差と軸上色収差のイメージの違いは下記となります。
レンズに関しては下記の記事も記載しておりますので、ご覧いただければ幸いです。
参考:【光学用語集】カメラモジュールに使われる、光学設計、レンズの基礎知識
参考:まずはこれだけで合格点。カメラを設計する為のレンズの基礎知識
参考:【カメラ】レンズの基礎知識入門、レンズ構成、レンズのスペックを分かりやすく解説
参考:【カメラ】レンズの基礎知識入門、解像力、MTF、空間周波数、TV解像度を解説
参考:【カメラ】レンズの基礎知識入門、撮像素子(イメージセンサ)における制約を解説
参考:【カメラ】レンズの基礎知識入門、ゴーストとレンズコーティングの関係を解説
記事が気に入って頂けたら、クリックして頂けると嬉しいです。


における制約を解説-150x150.jpg)
コメント